Knowledge for Data Analysis/통계 공부

[데이터 과학을 위한 통계] 탐색적 데이터 분석/EDA 과정

ddoddo201 2021. 9. 6. 22:58

 

[ 탐색적 데이터 분석: EDA ]

 

교재: 데이터 과학을 위한 통계(2판)

 

우리는 사물 인터넷(IoT, Internet of things) 세상에 살고 있다. 그 안에서 텍스트, 이미지, 비디오 등 수많은 소스로부터 비정형(=가공되지 않은) 데이터를 얻고 있다. 데이터 분석을 위해서는 정형 데이터로 변환 을 해야하고 분포를 확인 하는 과정이 매우 중요하다.

 

 

📍EDA(Exploratory Data Analysis, 탐색적 데이터 분석)

데이터를 이해하기 위해서 그래프, 통계자료를 이용하여 자료를 직관적으로 해석하는 과정이다.

EDA 과정을 보기 전에, 정형 데이터와 테이블 데이터에 대해서 먼저 정리하자.

 

▪️정형 데이터의 종류

 

(1) 수치형 데이터

  • 연속형 - 풍속, 시간 같은 연속적인 숫자
  • 이산형 - 사건의 발생 빈도 같은 이산적인 숫자

 

(2) 범주형 데이터

  • 이진형 - 예/아니오, 참/거짓 같이 두 개의 범주를 갖는 경우
  • 순서형 - 평점(1~5)처럼 범주 안의 값들이 순위를 갖는 경우

 

▪️테이블 데이터(Rectangular Data)

  • 데이터 분석에서 가장 많이 사용되는 형태로 행(record)와 열(feature)로 이루어진 이차원 행렬
  • 엑셀 스프레드시트, 데이터베이스의 테이블

 

 

 

그럼, EDA에 사용되는 방법들을 알아보자.

 

 

 

1️⃣ 위치 추정

데이터를 살펴보기 위해서, 가장 먼저 변수의 대푯값(typical value)을 구해야 한다.

이는 값의 중심경향성(=어디쯤에 위치하는지)을 나타내는 추정값이며, 다양한 값을 이용할 수 있다.

 

*특잇값(outlier): 일반적인 값과 매우 다른 데이터 값으로, 극단값으로도 부른다.

*로버스트하다(robust): 극단값에 민감하지 않다는 의미로, 저항성이 있다고도 말한다.

 

1. 평균

  • 가장 기본적인 위치 추정 방법이지만 데이터에 매우 민감하다
  • (모든 값의 총합) / (데이터의 개수)

 

2. 절사평균 (극단값에 민감하지 않음)

  • 값들을 크기 순으로 정렬한 후, 양끝의 일정 개수의 값들을 삭제 하고 구한 평균
  • 극단값의 영향을 피할 수 있으므로 평균 보다 선호하는 방식임
  • ex) 상위 하위 10%를 잘라내고 구한 평균

 

3. 가중평균

  • 각 데이터에 가중치를 곱하여서 구한 평균
  • (가중치*데이터의 총합) / (가중치의 총합)
  • 가중평균은 정확도 와 데이터 균형 을 맞추는데에 사용할 수 있다.
  • (데이터 균형의 관점) 데이터가 부족한 부분에 대해서 더 높은 가중치를 줄 수 있다.
  • (정확도의 관점) 정확도가 떨어지는 데이터에는 더 작은 가중치를 줄 수 있다.

 

4. 중간값 (극단값에 민감하지 않음)

  • 데이터를 정렬했을 때, 가운데에 위치하는 값

 

5. 가중 중간값 (극단값에 민감하지 않음)

  • 정렬 후 어떤 위치를 기준으로 상위 절반의 가중치 합과 하위 절반의 가중치 합이 동일해짐

 

< R실습 코드 >

mean(state[['Population']]) #평균
mean(state[['Population']], trim=0.1) #절사평균(상위 하위 10%를 잘라내고 구한 평균)
median(state[['Population']]) #중간값
#Population(인구)를 가중치로 두고 가중평균과 가중 중간값 구하기
weighted.mean(state[['Murder.Rate']], w=state[['Population']]) #가중평균
library('matrixStats')
weightedMedian(state[['Murder.Rate']], w=state[['Population']]) #가중 중간값

 

 

 

 

2️⃣ 변이 추정

데이터의 특징(데이터가 얼마나 밀집한지 혹은 퍼져 있는지를 나타내는 산포도)을 요약하는 방법이다.

 

1.평균절대편차

  • 편차들의 대표값 추정
  • (편차의 절대값의 합) / (데이터의 개수)*절댓값을 하는 이유 : 음의 편차가 양의 편차를 상쇄하므로 이를 막아줌
  • 편차: 해당값 - 평균

 

2. 분산과 표준편차

  • 분산 : 제곱편차의 평균 (= 편차 제곱의 합 / 데이터 개수)
  • 표준편차 : 분산의 제곱근

 

3. 중위절대편차 (극단값에 민감하지 않음)

  • |해당값-중간값| 집합의 중간값

 

4. 범위

  • 최대값 - 최소값 (=max-min)
  • 데이터가 얼마나 퍼져 있는지를 보여주지만, 특잇값에 매우 민감 해서 유용한 방법은 아니다.

5. 사분위범위(IQR)

  • Q3-Q1 = 제 3사분위수 - 제 1사분위수
  • 사분위수 : 자료를 동일한 비율로 4등분 할 때의 위치(25%, 50%, 75%)

 

< R실습 코드 >

sd(state[['Population']]) #표준편차(sd)
IQR(state[['Population']]) #사분위범위(IQR)
mad(state[['Population']]) #중위절대편차(MAD

 

 

3️⃣ 데이터의 분포 확인

1. 상자그림: 데이터의 분포(분산)을 쉽게 시각화하는 방법

quantile(state[['Murder.Rate']], p=c(.05, .25, .5, .75, .95)) #미국 주별 살인율의 백분위수
boxplot(state[['Population']]/1000000, ylab='Pupulation (millions)

- 인구의 중앙값(박스 안의 굵은 선) : 약 500만

- 수염(점선) : 데이터 전체의 범위

- 이상치(수염 바깥쪽) : 인구수가 높은 이상치가 존재함

 

 

 

2. 도수분포표: 어떤 구간에 해당하는 데이터들의 빈도

breaks <- seq(from=min(state[['Population']]), to=max(state[['Population']]), length=11)
options(scipen=5)
hist(state[['Population']], breaks=breaks)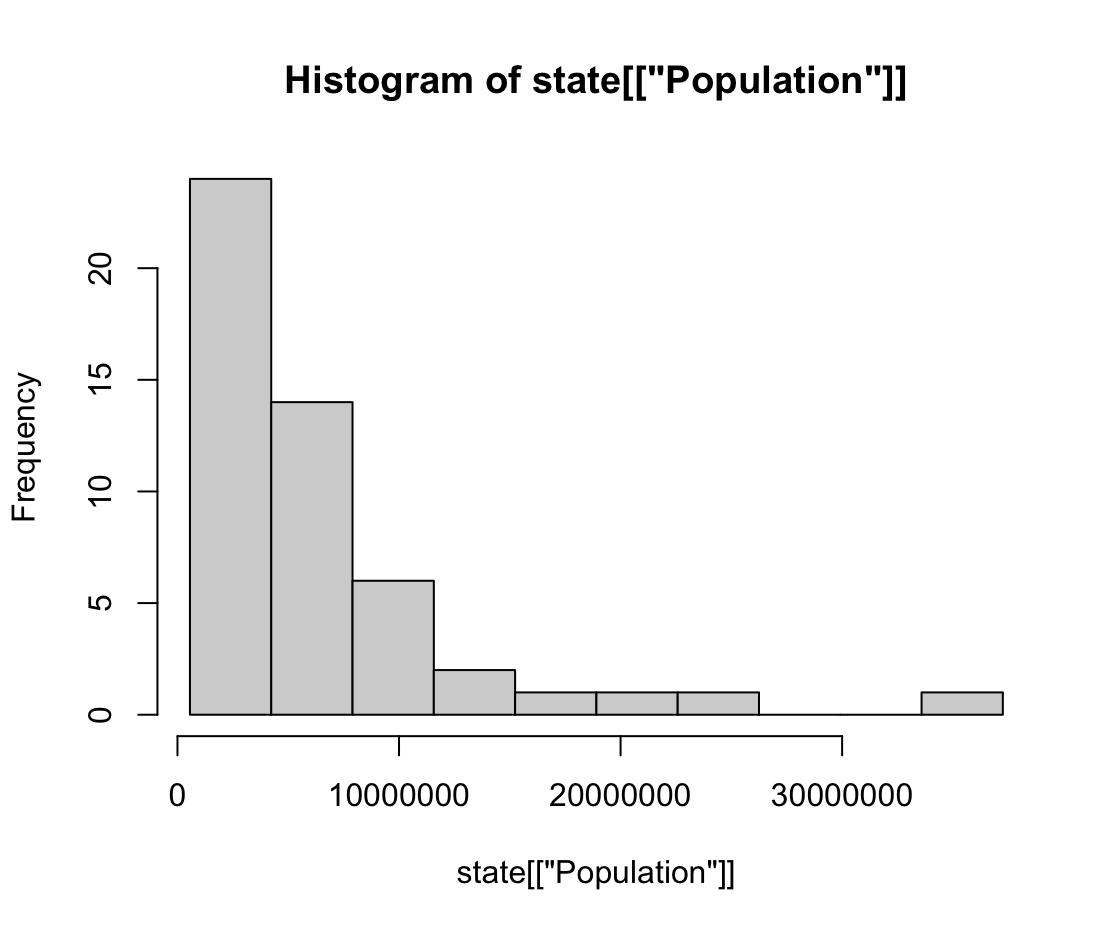

 

3. 히스토그램: x축(구간), y축(빈도수)에 대한 그림

 

4. 밀도 그림: 히스토그램을 곡선으로 나타낸 그림

 

 

 

 

 

 

데이터 분석 전에 자료를 해석하기 위해 EDA 과정을 진행하게 되며, EDA를 진행하기 위한 위치 추정/변이 추정/데이터의 분포 확인 과정을 배워보았다.

다양한 방법이 존재하지만 모두 데이터의 분포에 이상이 없는지 확인하는 과정이다. 

만약 이상치, 분포의 불균형, 치우침 등의 문제가 있으면 적절한 통계 함수를 사용해서 데이터를 정리해주게 되는데 이 부분에 대해서는 다음 시간에 배워보도록 하자😊😊