[Binary classification : Tabular data] / 3rd level / ROC-AUC

[Binary classification : Tabular data]

 

이 문제에서 모델의 성능을 확인하기 위해 📈ROC-AUC 지표를 확인하고 있다.

ROC-AUC를 이해하기 위해 필요한 개념들을 알아보자.

 

 

1️⃣ Positive, Negative의 기준은 어떻게 세우나?

일반적으로 예측해야 하는 것을 Positive 레이블로 설정한다.

 

*악성 종양이나 아니냐?

→ 악성 종양을 예측하는 것이 중요하다.

→ (Positive) 악성 종양 / (Negative) 악성이 아닌 종양

 

*대출 상환 가능한지?

→ 대출 상환을 못하는 사람을 찾는 것이 중요하다.

→ (Positive) 대출 상환 못하는 경우 / (Negative) 대출 상환 가능한 경우

 

 

 

 

2️⃣ TP, TN, FP, FN이란?

Confusion Matrix

 

🗣해석 방법 : (앞)예측을 맞췄는가 + (뒤)무엇으로 예측했는가

TP (True Positive): 정답 + Positive로 예측

TN (True Negative): 정답 + Negative로 예측

FP (False Positive): 오답 + Positive로 예측 (오답이므로 정답은 Negative)

FN (False Negative): 오답 + Negative로 예측 (오답이므로 정답은 Positive)

 

쉽게 말해서 정답을 맞춘 것은 (TP,TN)이고, 오답인 것은 (FP,FN)이다.

*좋은 모델은 정답을 맞추는 (TP,TN)은 높아야 하고 오답인(FP,FN)은 낮아야 한다.

 

 

 

 

3️⃣ FP, FN에 대하여

FP (False Positive): 실제로는 Negative인데 Positive로 예측한 경우 (=1종 오류)

• 실제로는 상환할 수 있지만(Negative) 상환 못할 것이라(Positive) 예측

 

FN (False Negative): 실제로는 Positive인데 Negative로 예측한 경우 (=2종 오류)

• 실제로는 상환 못하는데(Positive) 상환할 수 있다고(Negative) 예측

 

 

 

 

4️⃣ Accuracy(정확도)란?

일반적으로 모델 성능을 확인하는 지표로, 정답을 맞춘 비율을 확인한다.

*정답을 맞춘 것은 (TP,TN)이다.

 

 

 

 

5️⃣ 그럼 Accuracy(정확도)만 가지고 모델 성능을 판단하면 안되나?

정답 레이블이 불균형할 경우, 정확도 역설의 문제가 발생할 수 있다는 문제점이 있다.

 

💡정확도 역설이란?

만약 코로나 양성 5명, 음성 95명이 있다고 가정하자.

이때 모델 정확도는 높더라도 음성 환자 정답률은 100%, 양성 환자 정답률은 0%일 수 있다.

이는 양성 환자가 극히 드물어서(5명/100명) 정답을 맞추기 매우 어렵기 때문이다. 

그리고 상대적으로 음성 환자의 클래스가 많으므로(95명/100명) 음성 환자를 맞추는 일은 매우 쉽다.

 

이때, 우리는 코로나 양성(5명)을 맞추는 것이 중요하므로 모든 정답률을 비교해봐야 한다.

그래서 Precision, Recall, F1-score로 모델의 예측 성능을 평가하게 된다.

 

 

 

 

6️⃣ Precision(=PPV, Positive Predictive Value), Recall(=Sensitivity, Hit Rate)이란?

Precision은 예측 기준 정답률이고, Recall은 실제 정답 기준 정답률이다.

Precision ≒ Predict

Recall ≒ Real

 

 

 

*더 자세하게 알아보자.

아래 그림에는 2마리의 강아지가 있다.

이 때, 왼쪽 강아지는 'CAT'으로 잘못 분류 되었고 오른쪽 강아지는 'DOG'로 옳게 분류 되었다.

Precision (강아지로 예측된 것 중에 정답 비율) = 100%

Recall (실제 강아지인 것 중에 정답 비율) = 50%

 

 

 

 

7️⃣ Precision, Recall은 언제 중요할까?

경우에 따라 다른데, 몇가지 예시로 알아보자.

 

 

 

* 대출 상환 / 암 판정 / 금융 사기

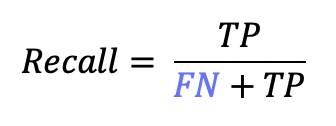
• 실제로는 상환 불가능한데(Positive) 상환 가능하다고(Negative) 예측되는 것은 위험하다.
• FN 을 낮춰야 한다.
• Recall 지표가 중요하다.

 

 

* 스팸 메일 분류하기

• 스팸 메일인데(Negative) 스팸이 아니라고(Positive) 분류되는 것은 위험하다.
• FP 를 낮춰야 한다.
• Precision 지표가 중요하다.

 

 

FP와 FN 중 어느 것이 더 위험한 지에 따라서 Precision이 더 중요할 수도 있고, Recall이 더 중요할 수도 있다.

 

 

 

 

 

8️⃣ F1-Score을 사용하는 이유는?

Precision, Recall은 상호 보완적이다. (한쪽이 높아지면 다른 한 쪽은 낮아지는 경향)

그래서 두 지표를 조화 평균한 F1-Score을 통해 최종 모델 성능을 확인하게 된다.

 

 

*상호 보완적인 이유

 

 

Precision 분모에는 FP가 있고, Recall의 분모에는 FN이 있음을 기억해라. (분모가 커지면 전체 값은 작아짐)

 

* FP 영역이 넓어지면 FN 은 줄어든다.

• (FP 증가) → Precision↓
• (FN 감소) → Recall ↑

 

* FP 영역이 줄어들면 FN 은 넓어진다.

• (FP 감소) → Precision ↑
• (FN 증가) → Recall ↓

 

 

 

 

9️⃣ ROC(=Receiver Operating Characteristic)곡선이란? 

먼저, TPR과 FPR을 알아야 한다.

TPR (True Positive Rate) = Recall

FPR (False Positive Rate) = 1-Specificity

 

*헷갈리지 않게 식으로 알아보자.

 

TPR (=Recall): 실제로 Positive인 것 중에 예측을 맞춘 비율

FPR (=1-Specificity): 실제로 Negative인 것 중에 예측을 틀린 비율

 

쉽게 말하자면 TPR은 정답률이고, FPR은 오답률이다.

좋은 모델이려면 정답률이 높아야 하므로 TPR이 높고, FPR이 낮아야 한다.

 

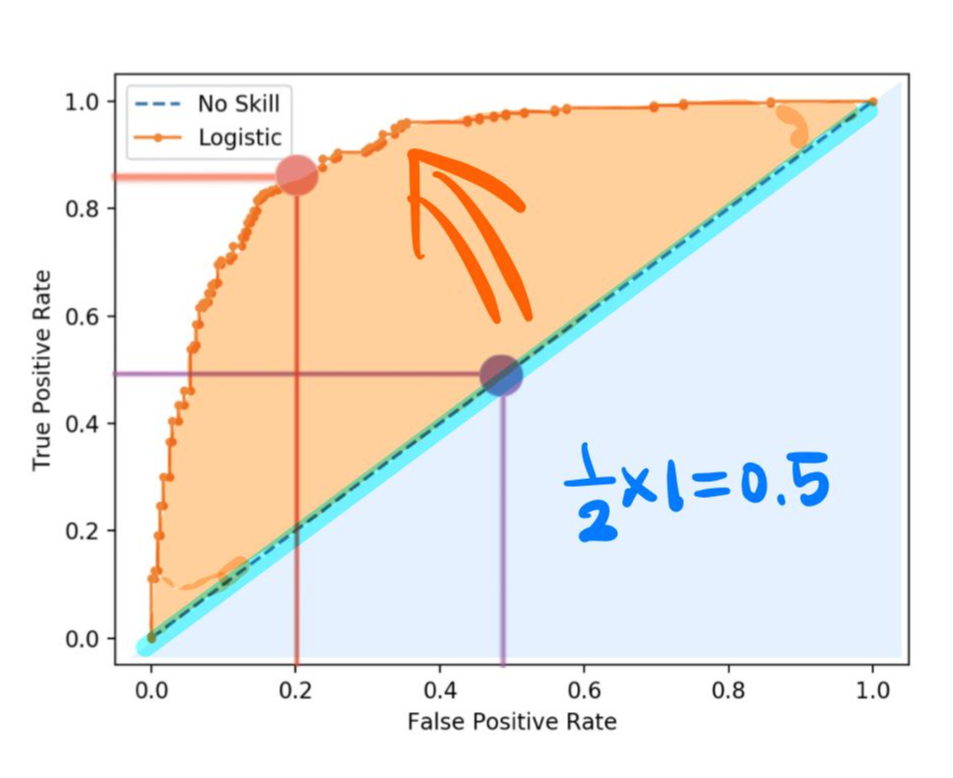
그럼 아래 ROC 커브에서 좋은 모델은 무엇일까?

파란색 직선 : TRP(0.5), FPR (0.5)

주황색 곡선: TPR (0.8), FPR (0.2)

 

좋은 모델은 TPR이 높고, FPR이 낮아야 하므로 주황색 곡선이 좋은 모델이다.

그렇기 때문에 일반적으로 가운데 직선으로부터 멀어질수록 성능이 좋다고 판단하는 것이다.

 

 

 

 

🔟 AUC(Area Under the ROC Curve) 지표란?

ROC 곡선 아래의 면적을 나타낸다.

가운데 직선에서 멀어질수록 좋은 모델이므로, AUC는 1에 가까울수록 좋은 모델이다.

 

*아래 총 면적은 1이고, 가운데 직선의 면적은 0.5이다.

*가운데 직선에서 멀어져야 하므로 0.5보다 크고 1에 가까워져야 한다.

AUC 면적에 따른 모델 성능 판단

• 0.9 ~ 1.0 : 아주 좋음
• 0.8 ~ 0.9 : 우수함
• 0.7 ~ 0.8 : 보통
• 0.6 ~ 0.7 : 괜찮지만 좋진 않음
• 0.5 ~ 0.6 : 좋지 않음

 

 

 

 

ROC 곡선과 AUC 지표를 해석하기 위해서 많은 개념을 알아보았다.

 

단순하게 "ROC가 직선에서 멀어질수록, AUC가 1에 가까울수록 좋은 모델이다"라고 공부한다면 

"왜 그러한가?"라는 질문에 답을 할 수 없을 것이다.

 

개념을 확실하게 알았으니 코드 필사를 해보자.

 

 

 

오차행렬 이미지 출처 https://manisha-sirsat.blogspot.com/2019/04/confusion-matrix.html

ROC 곡선 이미지 출처 https://driip.me/3ef36050-f5a3-41ea-9f23-874afe665342